EJEMPLFO F. LOGARÍTIMICA

Ante de conocer ejemplos sobre funciones logarítmicas, daremos un vistazo a sus definiciones. Definición

Sea a un real positivo fijo, y sea x cualquier real positivo, entonces:  La función que hace corresponder a cada número real positivo su  logaritmo en base  ,  denotada por  ,se llama: función logarítmica de base a,  y, el número  se llama logaritmo de x en la base a.  La definición anterior, muchas veces, se expresa diciendo que :el logaritmo de un número,  en una base dada ,es el exponente al cual se debe elevar la base para obtener  el número.  En el teorema siguiente, se presentan las propiedades más importantes de los  logaritmos.   Teorema ( Propiedades de los logaritmos ) Si a > 0, y b es cualquier real positivo, x e y reales positivos, entonces :   .  .  Cuando a > 1 , si 0 < x < y , entonces,  .Es decir ,la función  logarítmica de base a > 1 es estrictamente creciente en su dominio.  Cuando 0 < a < 1, si 0 < x < y ,entonces,  .Esto es la función  logarítmica de base entre 0 y 1; es estrictamente decreciente en su dominio.  Para todo número real , existe un único número real   tal que . Esta propiedad indica que la función logarítmica es sobreyectiva .  .  Si  , y, a != 0 , entonces, . (Invarianza)  Demostración. Para demostrar las propiedades de los logaritmos, se hace uso de  la definición y de las propiedades de la función exponencial, presentadas  en la sección anterior.  A manera de ilustración , se demuestran las propiedades 1,4 y 7. Se dejan  las restantes como ejercicio para el lector.   Sea  .De acuerdo a la definición de logaritmo y de la propiedad 9  del teorema 3 ,se tiene :  .  Esto es ,  ( 1 )  En segundo lugar , nuevamente por la definición , .  0 Es decir ,  ( 2 ).  De ( 1 ) y ( 2 ), se concluye que .  Sea  y  , entonces :   ( 1 ).   ( 2 ).  De ( 1 ) y ( 2 ), se sigue que :  .  Es decir , .  7.Se supone que a > 1 y 0< x < y. Sean :  y  .Se prueba que   .  En efecto ,si  ,y como a > 1 ,se tendría por la propiedad 7 del  teorema 3 que , es decir ,  en contradicción con la hipótesis.  Análogamente, se razona para el caso 0 < a < 1.  Observaciones. i ) La igualdad , dada en la propiedad 1, es también válida para b < 0 .  ii) Las propiedades 7 y 8 de los logaritmos, conjuntamente con las propiedades 7 y 8 de los exponentes, ponen     de manifiesto el comportamiento similar que presentan las funciones  exponenciales y logarítmicas en una misma     base .Es decir, si una de ellas es continua y creciente  ( continua y decreciente ) , la otra también lo es.  iii) La base más frecuentemente utilizada para las funciones exponenciales y  logarítmicas es el llamado número      e (número de EULER ).Los logaritmos de base e son llamados  logaritmos Naturales o Neperianos y se      denotan por Ln .Sin embargo ,los que más a menudo se encuentran  tabulados y que se utilizan en la practica son     los  correspondientes a la base 10 ,los cuales son llamados  logaritmos decimales o vulgares y se denotan       por   o,   simplemente, Log x.        Gráfica de La Función Logarítmica  En las figuras 3 y 4 , aparecen las gráficas de las funciones  e  , en concordancia con las propiedades establecidas en  el teorema inmediatamente anterior.  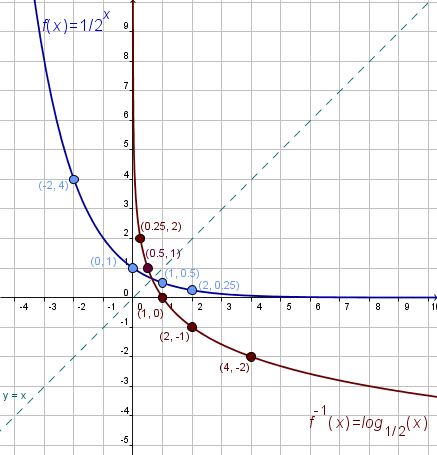En la figura 5, se han trazado conjuntamente las curvas  e    .Allí pueden visualizarse los comentarios hechos en la observación  ii). Puede notarse, además, que las curvas son simétricas con respecto a la  recta y = x.

Ejemplo 1:
Encontrar una tabla de valores para $f$ x = log2 x
Solución:
Sabemos que la función $f$ x = log 2 x es la inversa de $f$ x = 2 x
Una tabla de valores de $f$ x = 2 x es:

x	-3	-2	-1	0	1	2	3
$f$ x = 2 x	$1$ 8	$1$ 4	$1$ 2	1	2	4	8

Entonces, una tabla de valores de $f^{-1}$ x = log 2 x es:

x	$1$ 8	$1$ 4	$1$ 2	1	2	4	8
$f$ - 1 x = log 2 x	-3	-2	-1	0	1	2	3

Ejemplo 2:
Encontrar una tabla de valores para $f$ x = log 3 x
Solución:
La función $f$ x = log 3 x , es la inversa de $f$ x = 3 x
Una tabla de valores de $f$ x = 3 x es: 

x	-3	-2	-1	0	1	2	3
$f$ x = 3 x	$1$ 27	$1$ 9	$1$ 3	1	3	9	27

Entonces, una tabla de valores de $f^{-1}$ x = log 3 x es:

x	$1$ 27	$1$ 9	$1$ 3	1	3	9	27
$f$ - 1 x = log 3 x	-3	-2	-1	0	1	2	3

Ejemplo 3:
Encontrar la gráfica de la inversa de la función exponencial $f$ x = 12 x representada en la siguiente figura:

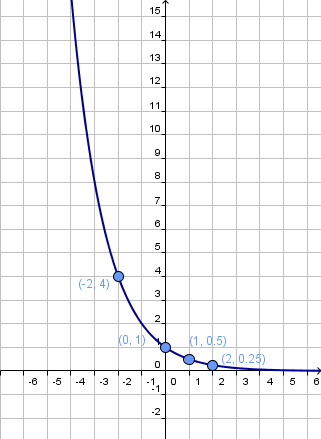Solución:
Sabemos que la inversa de $f$ x = 12 x es $f^{-1}$ x = log 12 x . Para graficar $f^{-1}$ x = log 12 x , ubiquemos algunos puntos en la gráfica y construyamos una tabla:

x -2 -1 0 1 2 $f$ x = 12 x 4 2 1 $1$ 2 $1$ 4 De la tabla anterior, obtenemos la tabla que corresponde a $f$ - 1 partir de esta tabla, trazamos la gráfica correspondiente: x 4 2 1 $1$ 2 $1$ 4 $log$ 12 x -2 -1 0 1 2 La figura a la derecha muestra la gráfica de la función inversa en rojo, la función f en azul. Note que las gráficas son simétricas con respecto a la recta y=x por ser funciones inversas.